电子气体的简并压计算与钱德拉塞卡极限推导

在固体物理学中，电子气体是一种由大量自由电子组成的系统，它们受到量子力学的影响。简并压指的是由于电子波函数的重叠导致的压力，可通过简并态数目计算得出。其计算公式如下：

简并压 P = (2/5) * (π^2) * (ħ^2) * (n^(5/3)) / (m)

其中，P 为简并压，ħ 为约化普朗克常数，n为电子密度，m为电子质量。

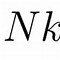
在统计力学中，钱德拉塞卡极限描述了玻色爱因斯坦凝聚中粒子量子态的最大可能数目。其推导过程如下：

根据波尔兹曼分布，粒子数目随能量的分布满足：

N(E) = (2^(s 1)) * π * (E^(s/2)) / ((s 1)!) * ((ħ^2) / (2m))^(s/2) * V

其中，N(E)为能量为E的量子态数目，s为系统的维度，V为系统体积。

然后根据能级密度，我们可以得到单位能量间隔内的量子态数目：

D(E) = dN(E) / dE = (s/2) * N(E) / E

最终，钱德拉塞卡极限即取极值时的量子态数目，满足条件：

dD(E) / dE = 0

通过求解以上方程，我们可以得到钱德拉塞卡极限下的最大量子态数目。

以上是关于电子气体的简并压计算与钱德拉塞卡极限的基本内容及推导过程。