国际月球科学空间站

计算电子气体的简并压（或费米压）可以利用统计物理学中的费米气体模型。在固体物理学中，我们常用费米气体模型来描述电子在固体中的行为，其中简并压是一个重要的物理量。

1. 费米气体模型概述

费米气体是一种由费米子（如电子）组成的量子气体，其特点是根据泡利不相容原理，每个量子态只能被占据一个费米子。在零温下，费米子填充能级遵循费米狄拉克分布，即填充状态密度从费米能级开始逐渐填充，直到所有的费米子都被分配到最低的能态为止。

2. 简并压的计算

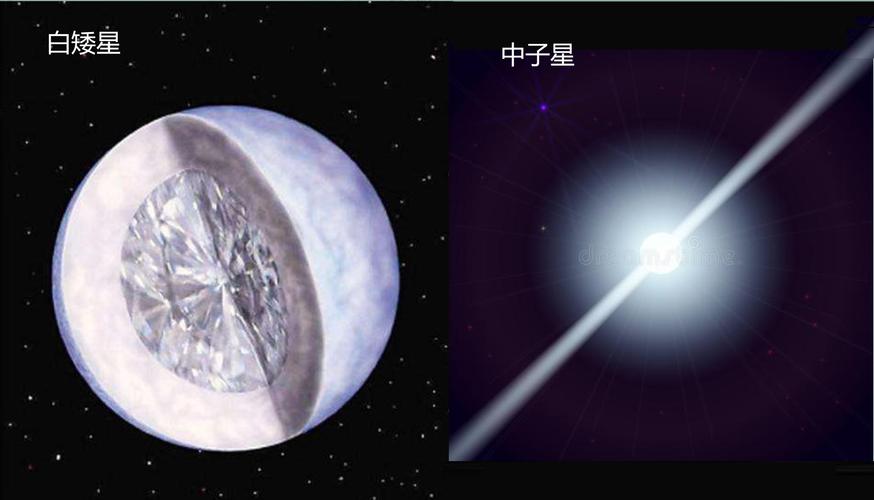
简并压（或费米压）可以通过费米能级的概念来定义和计算。费米能级是指在零温下，处于半满状态的最高能级。费米气体的压强（简并压）可以通过费米能级的位置和电子的能态密度来计算。

推导钱德拉塞卡极限

钱德拉塞卡极限是指电子气体在零温度下达到的最大压力。这个极限对应于费米气体的状态，其中所有的能级都被填满到费米能级。在这种情况下，简并压（费米压）可以通过以下方式推导：

假设电子气体的费米能级为 \(\epsilon_F\)，其能态密度为 \(g(\epsilon)\)，简并度为 \(g\)。在零温下，简并压 \(P\) 可以表示为：

\[ P = \int_0^{\epsilon_F} g(\epsilon) \cdot \epsilon \cdot \frac{d g(\epsilon)}{d \epsilon} d\epsilon \]

这里的 \(g(\epsilon)\) 是费米气体的态密度，即单位能量范围内的能态数目。费米能级 \(\epsilon_F\) 对应于电子的化学势（或费米能量），在零温下，化学势就是费米能级。

张朝阳的物理课推导

张朝阳在其物理课程中可能会详细讲解如何推导钱德拉塞卡极限。一般来说，推导的关键点包括：

费米狄拉克分布的应用，即零温下费米子填充状态的分布。

费米能级的定义和计算，即最高被占据的能级。

使用能态密度函数 \(g(\epsilon)\) 计算简并压 \(P\)。

结论

电子气体的简并压是理解固体物理学中电子行为的重要概念。在理论和实验研究中，对简并压的准确计算和理解有助于解释和预测材料的电子性质和行为。张朝阳的物理课可能会深入探讨这些理论，并帮助学生理解费米气体模型及其在实际物理现象中的应用。

如果你需要更详细的推导或具体数学细节，可以查阅相关的固体物理学教材或学术文献，这些资源通常会提供详细的数学推导和物理背景。